1(2) 2008
 |
|
 |
ARCHITECTURE AND MODERN INFORMATION TECHNOLOGIES
МЕЖДУНАРОДНЫЙ ЭЛЕКТРОННЫЙ НАУЧНО-ОБРАЗОВАТЕЛЬНЫЙ ЖУРНАЛ ПО НАУЧНО-ТЕХНИЧЕСКИМ И УЧЕБНО-МЕТОДИЧЕСКИМ АСПЕКТАМ СОВРЕМЕННОГО АРХИТЕКТУРНОГО ОБРАЗОВАНИЯ И ПРОЕКТИРОВАНИЯ С ИСПОЛЬЗОВАНИЕМ ВИДЕО И КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ
THE COMPUTER METHODS OF CONSTRUCTION SPIRAL STRUCTURESМЕТОД АВТОМАТИЗИРОВАННОГО ГЕОМЕТРИЧЕСКОГО ПОСТРОЕНИЯ СПИРАЛЬНЫХ СТРУКТУР
А.В. Радзюкевич
Новосибирская государственная архитектурно-художественная академия, Новосибирск, Россия
Спиральные структуры являются объектом изучения большого количества наук, в том числе и архитектурной бионики [1, 2]. Спиральное расположение семян, листьев, веток, чешуек, называемое филлотаксисом является весьма распространенным в природе явлением (рис.1).
|
Рис. 1. Явление филлотаксиса в природе |
В качестве биологического объекта, строение которого можно наглядно описать с помощью спиральных структур, как правило, используется корзинка подсолнуха. Элементарные эмпирические наблюдения дают возможность предположить, что корзинка подсолнуха состоит из однотипных четырехугольных ячеек, «растущих» от центра к периферии.
Зададимся вопросом: можно ли по аналогии с укладкой семечек в корзинке подсолнуха беспустотно заполнить плоскость однотипными геометрическими фигурами, которые отличаются друг от друга только масштабом и углом поворота относительно некоторой центральной точки? Для ответа на этот вопрос попытаемся создать геометрическую модель построения таких фигур. Следуя аналогии с подсолнухом, определим основные элементы модели. Предположим, что относительно некоторой точки, назовем ее полюсом “О”, построено некоторое количество правых и левых спиралей, которые равномерно распределены по окружности (рис. 2). Будем считать, что спирали являются логарифмическими. Получаем, что плоскость заполняется однотипными фигурами, “растущими” от центра к краям. Каждая такая фигура ограничивается двумя соседними правыми и двумя соседними левыми спиралями. Пересекаются эти спирали в четырех точках. Заменим криволинейные части спиралей на отрезки, соединяющие точки пересечения спиралей. В этом случае получаем беспустотное заполнение плоскости четырехугольниками “растущими” от центра к периферии (рис. 2).
 |
|
Рис. 2. Геометрическое моделирование спиральной решетки на плоскости |
Проверим, можно ли произвести однозначное математическое построение таких четырехугольных однотипных ячеек? Для построения геометрической модели зададим для нее следующие параметры:
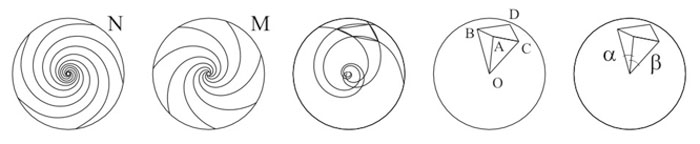
1. Примем, что спиральная решетка образуется на основе N правых логарифмических спиралей и М левых логарифмических спиралей (рис. 3);
2. Центр спиралей или полюс обозначим буквой О;
3. Обозначим точками А, В, С, D точки пересечения двух пар соседних правых и левых спиралей;
4. Обозначим угол AОB как угол альфа_1, а угол ,
при этом и AОC как угол бета_1.
 |
|
Рис. 3. Геометрическое моделирование ячейки спиральной решетки |
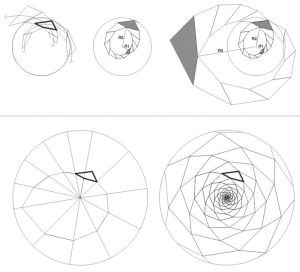
Только при соблюдении этих условий, по нашим исследованиям, многократное масштабное копирование четырехугольника ABCD по часовой стрелке и против часовой стрелки позволит беспустотно заполнить плоскость (рис. 4). Следует отметить, что копирование исходного четырехугольника N раз по часовой стрелке и M раз против часовой стрелки приводит к замыканию спиралей. Продолжая копирование, получаем новый виток с новым замыканием спирали. При этом расстояние от четырехугольника до полюса спиралей точки О будет изменяться на постоянную величину
R2/R1=R3/R2=R(n+1)/R(n).
Назовем эту величину коэффициентом роста спиральной решетки.
 |
|
Рис. 4. Геометрическое построение спиральной решетки, беспустотно заполняющей плоскость |
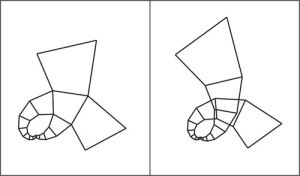
Несоблюдение обозначенных условий приводит к тому, что «замыкания» спиралей не происходит (рис. 5).
 |
|
Рис. 5. Пример геометрического заполнения плоскости спиральной решеткой с произвольными параметрами |
 |
Рис. 6. Примеры спиральных решеток, имеющих различные формы ячеек |
Попытаемся задать какие-либо граничные условия для построения спиральных решеток. Сформируем модель, в которой точки пересечения спиралей (вершины ячеек) будут являться центрами касающихся друг друга окружностей (условно назовем их шариками, центры которых лежат в одной плоскости). В этом случае, при соблюдении определенных условий также возможно построение неограниченного количества спиральных решеток. Для расчета геометрических параметров таких решеток нами был составлен алгоритм вычислений, основанный на решении весьма громоздкой системы тригонометрических уравнений. Автоматизированный расчет производилось с помощью программы MatCAD (автор алгоритма С.В.Щербатых). Полученные результаты расчетов по заданным количествам значений N и M служили основой для графического изображения решеток. Проблема трудоемкости геометрических построений была решена с помощью автоматизации этого процесса на основе программного модуля AutoLISP программы AutoCAD (автор алгоритма С.А.Мороз).
При фиксированных значениях N и M, величина коэффициента роста спиралей может быть любой, но только внутри определенных пределов. Пределы возникают в тех случаях, когда происходит касание шариков, расположенных в противоположных вершинах ячейки. В этом случае полярно-тетрагональная структура превращается в полярно-гексагональную и получается только два варианта раскладки шариков. В первом случае касаются дальний и ближний, относительно центра спиралей, шарики. Во втором случае происходит касание боковых шариков.
Рассмотрим, каковы особенности и свойства полярно-гексагональных спиральных решеток. Предположим, что сумма правых и левых спиралей являет величиной постоянной и равна, допустим, восьми. В этом случае, теоретически, имеем девять вариантов построения спиральных решеток:
1) 8M(4) – 0N(4);
2) 7M(4) – 1N(4);
3) 6M(4) – 2N(4);
4) 5M(4) – 3N(4);
5) 4M(4) – 4N(4);
6) 3M(4) – 5N(4);
7) 2M(4) – 6N(4);
8) 1M(4) – 7N(4);
9) 0M(4) – 8N(4)
Если отбросить взаимно симметричные варианты, то останется только пять вариантов:
1) 8M(4) – 0N(4);
2) 7M(4) – 1N(4);
3) 6M(4) – 2N(4);
4) 5M(4) – 3N(4);
5) 4M(4) – 4N(4)
Случай № 1 можно назвать спиральной решеткой с некоторой натяжкой, так как в одном направлении спирали практически нет, и она превращается в окружность. Но, тем не менее, мы рассмотрим этот случай для выстраивания полной панорамы всех типологических случаев. Тем более что данная структура фактически является радиально-кольцевой. Это представляет отдельный исследовательский интерес, так как именно такова градостроительная структура многих исторических городов.
Мы попытались определить, как соотносятся между собой некоторые геометрические характеристики различных спиральных решеток. В частности, мы рассмотрели, как соотносятся периметры ячеек с их площадями (рис. 7). Для соразмерения этих величин, длины и площади, периметр делился на величину корня квадратного от площади ячейки. Результаты показали, что относительную максимальную площадь имеет ячейка спиральной решетки при максимальном различии количества правых и левых спиралей (N=0, M=8). Очевидно, что увеличение значения М, приведет к увеличению относительной площади ячейки, так как она, в пределе, будет стремиться к форме правильного шестиугольника.
Кроме того, мы рассмотрели, как соотносится площадь “пустоты”, образуемой между окружностями ячейки, к площади самой ячейки. Оказалось, что в спиральной решетке, в которой N=M (назовем ее симметричной спиральной решеткой) относительная площадь пустоты оказалась минимальной. Следовательно, именно симметричные спиральные решетки обладают наибольшей плотностью укладки шариков
(рис. 7).
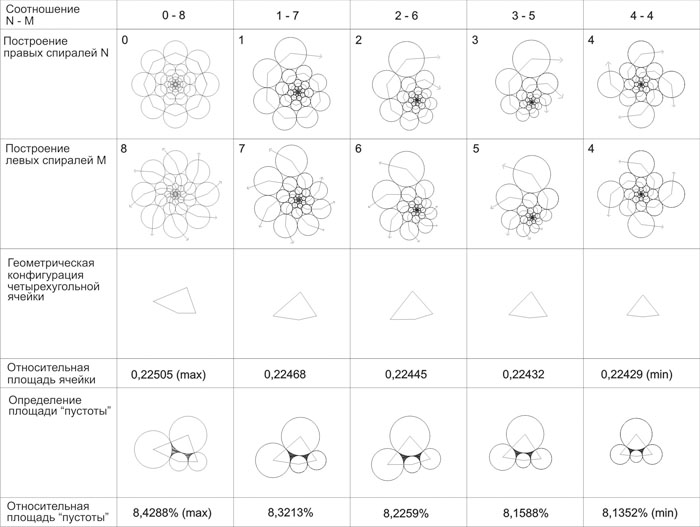 |
Рис. 7. Сопоставление геометрических параметров различных спиральных решеток
Следует обратить внимание на то, что в природных объектах ячейки могут иметь не четырехугольную, а шестиугольную форму, как это наблюдается в корзинке цветка маргаритки. Здесь получилась, условно говоря, полярно-сотовая структура укладки элементов. Выведенный нами алгоритм расчета построения спиральных полярно-гексагональных структур, дает нам возможность построения спиральных структур из шестиугольников.
По аналогии с построением различных спиральных решеток, основанных на четырехугольных ячейках (рис. 7), нами были построены спиральные решетки, основанные на шестиугольных ячейках.
Проверка геометрических характеристик шестиугольных ячеек, показала, что они идентичны параметрам решеток, построенных на базе четырехугольных ячеек. Минимальная площадь пустот по отношению к шестиугольной ячейке оказалась, как и ранее, в том случае, когда количество правых и левых спиралей равно. Максимальная площадь шестиугольной ячейки по отношению к периметру получилась аналогично в том случае, когда соотношение встречных спиралей предельно различно (N=0 и M=8). Следует отметить, что в зависимости от определенных заданных условий шестиугольные ячейки также как и четырехугольные ячейки могут иметь выпуклую и «вогнутую» форму, а также, в случае нахождения двух сторон шестиугольника на одной прямой, могут превратиться в пятиугольники.
Зададимся очередным вопросом: можно ли решить задачу по нахождению идеальной планировочной структуры города, в котором длина дорог будет минимальной по отношению к площади участков, заключенных между этими дорогами. Очевидно, что на основе декартовой системы координат, идеальными будут две структуры - тетрагональная и гексагональная, на основе квадрата и правильного шестиугольника. В первом случае относительная площадь участка будет равна 0,25 единицам, а во втором – 0,26864 единицам. Перебрав все полярно-тетрагональные (рис. 8) и полярно-гексагональные (рис. 9) спиральные структуры, имеющие экстремальные параметры, получаем, что наиболее оптимальной структурой следует считать спиральную структуру с количеством спиралей N=0 и M=8.
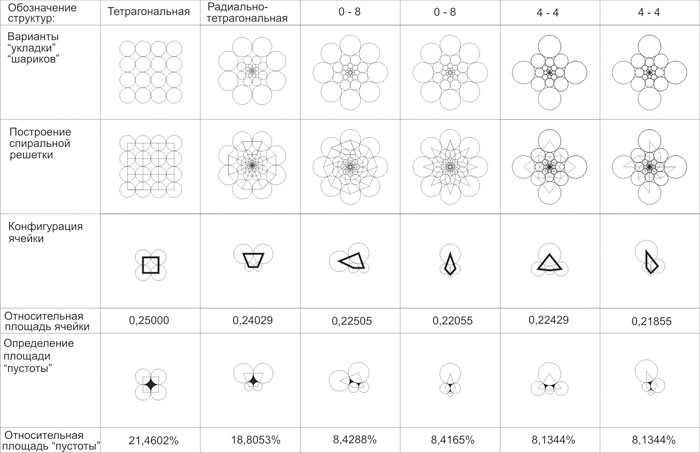 |
Рис. 8. Сравнение геометрических параметров радиально-тетрагональных спиральных решеток
Условно назовем ее радиально-гексагональной. В этом случае, относительная площадь ячейки будет максимальной по сравнению со всеми другими вариантами – 0,26517. Она уступает гексагональной структуре всего на 1,3% и превосходит тетрагональную структуру на 5,7%.
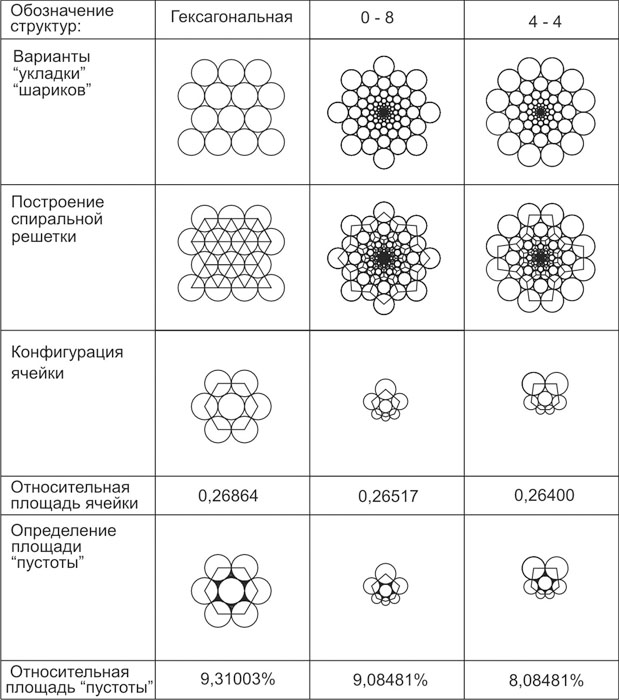 |
Рис. 9. Сравнение геометрических параметров радиально-гексагональных спиральных решеток
Такое превышение следует считать весьма существенным в плане решения задач по поиску оптимальных градостроительно-планировочных структур. Вероятно, в данном абстрактно-теоретическом подходе есть определенный прикладной экономический смысл. Тем более, что похожее решение уже было предложено архитектором Антонио Филарете еще в 15 веке, при определении конфигурации идеального города – Сфорцинды [3] (рис. 10).
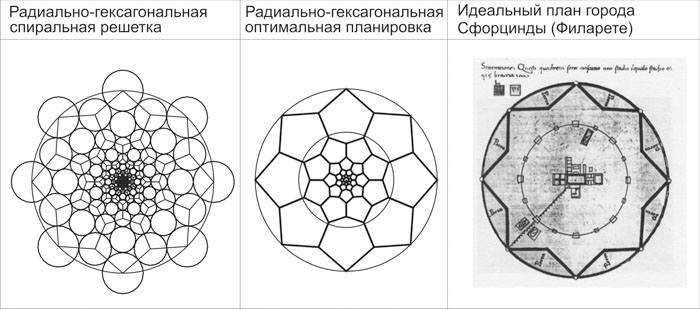 |
Рис.10. Сравнение оптимальной радиально-гексагональной спиральной структуры с планом идеального города Сфорцинды (А.Филарете)
Нами также были проведены сопоставления геометрических параметров различных спиральных решеток с целью выявления тех или иных экстремальных (максимальных или минимальных) значений. В частности, интерес представляли спиральные решетки с соотношением количества встречных спиралей близким к пропорции «золотого сечения». Однако из всех рассмотренных вариантов, вариант ближайший к «золотому сечению» (N=3, M=5) не оказался экстремальным по определенным нами параметрам. Следовательно, в природных объектах укладку семян нельзя признать максимально плотной. Нельзя также утверждать, что площадь ячейки (четырехугольной или шестиугольной) является предельно максимальной по отношению к величине периметра (стенок) ячейки.
В заключение можно сказать, что данная работа дает возможность для практического выхода на решение целого ряда прикладных архитектурно-дизайнерских задач. В частности, разработанный метод расчета формы ячеек, позволит упорядочить процесс геометрического структурирования и формообразования в различных сферах дизайна (орнамент, декор и т.д.). Кроме того, его можно использовать в градостроительстве. Приведенные сопоставления различных геометрических структур дают возможность утверждать, что радиально-гексагональные структуры является наиболее оптимальными, по критерию минимизации длины периметров (путей, дорог, коммуникаций). При этом в них получается максимальная относительная площадь ячеек (кварталов, районов).
Возникает еще один вопрос: почему же тогда природа не “выбрала” радиально-гексагональную структуру для формирования живых объектов? По всей видимости, здесь мы имеем дело с разными стратегиями роста структур. Так, если рассматривать процессы роста города, то можно утверждать, что они основаны на одновременном росте по нескольким направлениям от центра к периферии. И в этом случае происходит присоединение новых территорий. Нечто похожее происходит, очевидно, и в случае роста кристаллов. А в биологических объектах, например в корзинке подсолнуха, процесс роста осуществляется по другому сценарию. В центре корзинки через равные промежутки времени происходит формирование новых семечек, которые в процессе выталкивания новыми семечками, занимают тот сектор корзинки, который является более свободным от других семечек. Наглядно, в огрубленном виде этот процесс можно наблюдать в виде ролика, выставленного на одном из сайтов [4] (программа FBN1NB). Математическое моделирование этого процесса [5], показало, что наиболее оптимальное заполнение корзинки возникающими и растущими семечками происходит в случае формирования спиральных решеток с соотношением количества правых и левых спиралей в пропорции “золотого сечения”.
Принципиальная разница между процессами роста кристаллов и роста биологических структур, очевидно, заключается в том, что в первом случае действует механизм “наращивания”, т.е. присоединения новых элементов извне, а во втором случае действует механизм “выталкивания” каждого нового элемента из центра к периферии.
Conclusions
This very investigation made it possible to define the main difference in the growing strategy of animate and inanimate structures. Spiral structures of animate issues are not maximum optimal from the point of view of geometry. Their optimum is based on the special strategy of elements growing in the centre and spread to the periphery under pressure.
These found spiral structures having maximum optimum (radial-tetragonal and radial-hexagonal) may be an optimal decision in town-planning.
The developed algorythm of automatized geometric building of spiral grids may be used in design (ornament, decoration, etc.)
Литература
1. Шубников А.В., Копцик В.А. Симметрия в науке и искусстве. Издание третье, дополненное. М.2004.
2. Архитектурная бионика. Под ред. Лебедева Ю.С. М. Стройиздат.1990.
3. Филарете (Антонио Аверлино). Трактат об архитектуре. Пер/прим. В.Л.Глазычев. Изд.”Русский университет”. М. 1999.
4. http://www.brantacan.org.uk/programs.htm
5. Щетников А.И. Проблемы филлотаксиса. http://www.nsu.ru/classics/pythagoras/Phyllotaxis.pdf















