1(2) 2008
 |
|
 |
ARCHITECTURE AND MODERN INFORMATION TECHNOLOGIES
МЕЖДУНАРОДНЫЙ ЭЛЕКТРОННЫЙ НАУЧНО-ОБРАЗОВАТЕЛЬНЫЙ ЖУРНАЛ ПО НАУЧНО-ТЕХНИЧЕСКИМ И УЧЕБНО-МЕТОДИЧЕСКИМ АСПЕКТАМ СОВРЕМЕННОГО АРХИТЕКТУРНОГО ОБРАЗОВАНИЯ И ПРОЕКТИРОВАНИЯ С ИСПОЛЬЗОВАНИЕМ ВИДЕО И КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ
TOPOLOGICAL METHOD OF CONSTRUCTION OF POINT SURFACES AS PHYSICAL MODELS
ТОПОЛОГИЧЕСКИЙ МЕТОД СОЗДАНИЯ ФИЗИЧЕСКИХ МОДЕЛЕЙ ТОЧЕЧНЫХ ПОВЕРХНОСТЕЙ
Д. Ю. Козлов
Научно-исследовательский институт теории архитектуры и градостроительства (НИИТАГ) Российской академии архитектуры и строительных наук (РААСН), Москва
Форма архитектурных объектов в наиболее общем случае может рассматриваться как оболочка — двумерная поверхность, вложенная в трёхмерное пространство. Непосредственно мы воспринимаем только поверхности как синтез последовательных «фотоснимков» — двумерных отпечатков на вогнутом экране сетчатки наших глаз. В XV веке итальянский архитектор и теоретик архитектуры Леон‑Батиста Альберти утверждал, что вся архитектура заключается в очертаниях (линиях) и конструкции (структуре) (в оригинальном латинском тексте «lineamenta et structura») [1]. Видимая форма (очертания) существует лишь благодаря скрытой от взоров структуре, всецело её определяющей. С определением Альберти согласуются и современные математические теории формы, проводящие чёткое различие между видом (shape) — внешней поверхностью, и собственно формой (form) — внутренней структурой [2]. Это различие приобретает крайне важное значение в исследованиях, посвященных моделированию и восприятию архитектурной формы, в том числе и относящихся к области архитектурной эндоскопии.
Топология, как наиболее общая разновидность геометрии, определяет поверхности в трёхмерном пространстве как двумерные многообразия — ориентируемые (двухсторонние поверхности) или же неориентируемые (односторонние поверхности). Еще в середине XIX века было доказано, что любое ориентируемое двумерное многообразие эквивалентно поверхности кренделя с некоторым числом дырок или же сфере с тем же числом ручек [3]. Число дырок или ручек есть «род поверхности» — топологический инвариант, который равен нулю для сферы, единице для тора (поверхности с одной дыркой), двум для кренделя с двумя дырами и т. д. Любая поверхность может быть разбита на некоторое количество двумерных ячеек или граней (F), разделённых между собой одномерными границами или рёбрами (E), которые, в свою очередь, пересекаются в нульмерных точках или вершинах (V). Эти три элемента разбиения любой поверхности взаимосвязаны между собой в соответствии с простейшим уравнением, называемым формулой Эйлера: V − E + F = 2 − 2n, где n — число рода поверхности. Например, для любого разбиения поверхности сферы — то есть для произвольного многогранника — значение формулы Эйлера равно двум, а для поверхности тора — соответственно равно нулю.
Топологический подход к проблеме физического или виртуального моделирования поверхностей позволяет провести различие между видом и формой так же, как и между очертанием и структурой. Более того, топология способна дать нам новые инструменты для описания, моделирования и практической работы с такими пространственными объектами, которые до сих пор пребывали лишь в области математических абстракций.
Моделирование поверхностей в архитектуре, так же, как и любых других поверхностей, следует общей логике нашего восприятия пространственных объектов. На практике для нас представляется более удобным работать с моделями на плоскости — рисунками, проекциями, перспективами или же с графическими образами на плоском дисплее компьютера. Точно также намного удобнее и практически создавать реальные поверхности трёхмерных объектов в двумерном пространстве в виде плоских заготовок их фрагментов, развёрток или выкроек. В результате, практические возможности физического моделирования поверхностей в пространстве во многом определяются формообразующими возможностями и структурой материала, выбранного для создания их плоских развёрток. В этом случае происходит практически полное совпадение визуально воспринимаемой формы и структуры, определяющей её пространственные свойства.
Развёртывающиеся поверхности представляют собой элементарный случай перехода от сплошной структуры плоского листа, такого как лист бумаги, металла или пластика, к фрагменту криволинейной поверхности в трёхмерном пространстве. К сожалению, развёртывающимися поверхностями могут быть лишь линейчатые поверхности, такие как конусы, цилиндры, либо поверхности, состоящие из касательных к некоторой пространственной кривой.
Возможно и разбиение плоскости сплошного листа на отдельные грани (фрагменты плоскости) и соединение их между собой шарнирными связями вдоль граничных рёбер, что приводит к созданию плоских развёрток складчатых поверхностей (Рис. 1). Но данный метод также ограничен: возможны лишь аппроксимации плоскими гранями трёхмерных криволинейных поверхностей (в основном выпуклых). Для более сложных поверхностей требуются плоские развёртки с разрезами и/или наложениями.
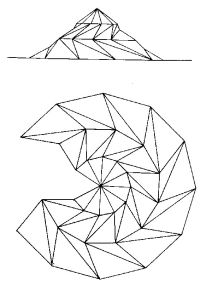 |
Рис. 1. Образование складчатых поверхностей из плоских развёрток
Другой известный подход заключается в отказе от сплошной модели плоскости в виде листа и переходе к её различным линейным аппроксимациям, то есть рёберным моделям, таким как ткани, сети и плоские решётки. Сами рёбра могут быть гибкими, упруго-эластичными или жёсткими и соединёнными между собой посредством трения или же с помощью шарниров. Известны различные структуры рёберных моделей плоскости, например тканевые, образованные переплетёнными взаимно ортогональными нитями основы и утка, вязаные сети с узлами, в частности рыболовные сети, плетёные конструкции из упруго-гибких стержней или прутьев, а также кинематические решётки из жёстких стержней, соединённых между собой подвижными шарнирами.
Принцип тканевой структуры нашёл широкое применение как в практическом моделировании сложных криволинейных поверхностей, так и в научной теории. Русский математик академик П. Л. Чебышев в 1878 г. установил математические принципы формообразования криволинейных поверхностей из плоских тканевых развёрток с квадратными ячейками [4], наглядно продемонстрировав, что поверхность шара может быть полностью покрыта двумя изначально плоскими выкройками. Другим важным направлением применения рёберных моделей плоскости в формообразовании криволинейных поверхностей является метод инверсии гибких висячих сетей, формируемых из плоского положения действием силы тяготения. Переворачивание висячей сети образует опорную поверхность безмоментной решётчатой оболочки (Рис. 2).
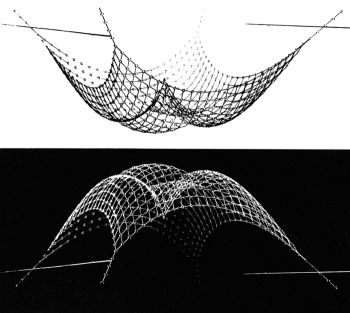 |
| Рис. 2. Формообразование сводчатых оболочек методом переворачивания висячих сетей |
Данный метод возник по аналогии с висячей цепью, принимающей форму цепной линии, которая, будучи перевёрнута, образует линию действия сил безмоментной арки. Знаменитый испанский архитектор А. Гауди в конце XIX века занимался систематическими экспериментами с висячими моделями из нитей, рассматривая их в качестве эффективного метода формообразования в архитектуре. Гауди искал конструктивные формы, которые позволили бы избавиться от действия моментов сил и сил сдвига, а также дали бы возможность зрителю непосредственно наблюдать распределение потоков сил в конструкции. В своих ранних работах Гауди аппроксимировал цепные линии параболическими арками, но позднее создал несколько висячих моделей для проектов церквей. Когда модели переворачивались, сформированные нитями многоугольники указывали направления для несущих опор [5].
В конце 40‑х годов прошлого века немецкий архитектор и инженер Ф. Отто начал свои собственные эксперименты с висячими моделями, выполненными из ткани пропитанной гипсовым раствором. Поначалу в его задачу входил лишь поиск форм для сводчатых покрытий, но в конце концов эти исследования заложили основу теории решётчатых оболочек, что позволило Ф. Отто и его сподвижникам создать целый ряд подлинных шедевров архитектуры XX века [5].
Тем не менее, модели плоскости на основе граней и рёбер не исчерпывают всех возможных аппроксимаций поверхности. Формула Эйлера для двумерных многообразий наглядно демонстрирует, что существуют всего три элемента топологического разбиения поверхности: двумерные грани, одномерные рёбра и нульмерные вершины. Следовательно, наряду с известными моделями плоскости, основанными на гранях и рёбрах, должна существовать и третья модель, образованная множеством вершин, или точечная модель плоскости (поверхности).
Модель отдельной изолированной точки может быть как виртуальной, так и физической. Виртуальная модель представляет собой лишь положение в пространстве, заданное тремя числовыми значениями относительно трёх декартовых координат. Именно этот метод задания точек используется в большинстве компьютерных программ и тем самым изначально закладывается во все созданные с их помощью модели.
В противоположность виртуальному методу, физическая модель точки представляет собой контакт или касание поверхностей реальных физических тел в реальном пространстве. Такие точечные контакты образуют, например, два касающихся твёрдых шара или два цилиндра с непараллельными осями вращения. Множество таких точечных контактов может рассматриваться как прототип физической модели, но построение реально функционирующей модели точечной поверхности обусловлено двумя существенными факторами. Во-первых, множество точечных контактов должно быть топологически связным, чтобы образованная ими модель поверхности была континуальной. Во-вторых, структура, связывающая между собой точечные контакты, должна допускать возможность их относительно независимого перемещения друг относительно друга. В частности, хорошей аппроксимацией фрагмента точечной поверхности может служить ткань из переплетённых упруго-эластичных стержней, наподобие поверхности корзины из свежих прутьев (Рис. 3), в которой присутствует множество точечных контактов между цилиндрическими телами.
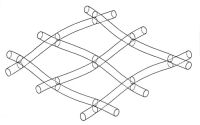 |
Рис. 3. Модель фрагмента точечной поверхности из переплетённых упруго-эластичных стержней
Но в пространстве такая структура действует подобно рёберной модели плоскости, поскольку её преобразование во фрагмент криволинейной поверхности происходит в результате деформации (изгибания) самих стержней или прутьев, а не как следствие движения точечных контактов. Таким образом, фрагментарная модель точечной поверхности еще не гарантирует её функционирование в качестве искомой модели трансформируемой поверхности, состоящей из подвижных точек‑вершин, так как в рассмотренной фрагментарной модели отсутствует наиболее существенная часть, а именно — топологически связная структура, физический носитель точечного множества.
Подчас сложные технические задачи, возникающие перед исследователем, оказываются уже давно решёнными в живой природе. Известно природное явление, связанное с работой упруго-гибких тканей, получившее в биомеханике название «резильянс» [6]. Оно связано с накоплением энергии упругости в материале конструкции, деформирующее его, но не вызывающее повреждений в самой конструкции. При этом возрастающая деформация материала приводит к увеличению несущей способности самой конструкции, снижению её веса и удлинению срока эксплуатации. Природные нитевидные упруго-эластичные протяжённые объекты, такие как полимерные молекулы, в частности молекулы ДНК, под действием их внутренней энергии упругости часто приобретают замкнутые циклические формы, при этом переплетаясь и перекрещиваясь сами с собой. В некоторых случаях эта тенденция приводит к образованию молекул в форме замкнутых топологических структур — колец и узлов, как отдельных, так и зацепленных между собой [7].
Эксперименты, проведённые автором с различными видами точечных моделей плоскости, подтвердили, что узлы и зацепления колец и узлов являются наиболее естественной формой самоорганизации и структуризации одномерно протяжённых упруго-эластичных объектов. Следствием этого факта является то, что естественной формой объединения системы независимых точечных контактов, заданных цилиндрическими соприкасающимися телами, является объединение их между собой связной топологической структурой, выполненной в виде циклического или периодического узла [8]. Упруго-эластичный стержень, длина которого на 2‑3 порядка превышает его диаметр, образует элементарную структуру, когда его концы соединяются между собой (Рис. 4a).
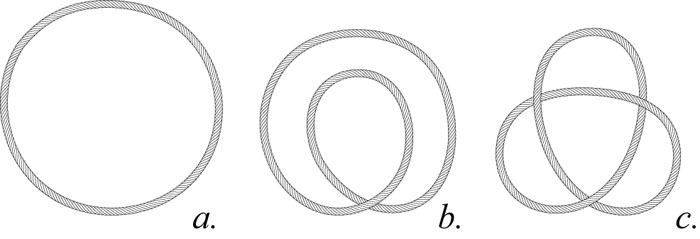 |
Рис. 4a. Кольцо (тривиальный узел) из упругого стержня
В результате стержень приобретает форму кольца (тривиального узла), и его конструктивная стабильность зависит от отношения диаметра самого кольца к диаметру образующего его стержня. Если диаметр кольца слишком велик по отношению к диаметру стержня, чтобы его внутренняя энергия упругости могла противостоять действию сил скручивания изогнутого стержня, то кольцо превращается в двойную вложенную петлю с одной перекрещивающейся точкой (Рис. 4b).
Рис. 4b. Двойная петля
Если же процесс образования вложенных петель происходит одновременно с соединением между собой концов стержня, то петли могут оказаться переплетёнными между собой, в результате чего замкнутый стержень станет заузленным, например в виде простейшего узла, называемого «трилистник» (Рис. 4c).
Рис. 4c. Простейший узел — трилистник
Явление «самозаузливания» типично для длинных упруго-эластичных одномерно протяжённых объектов, таких как стальная проволока или леска. Не случайно, что и живая природа выбрала этот топологический способ самоорганизации и естественного структурообразования.
Трилистник является не только простейшим узлом, но также и «торическим» узлом, так как его проекция может быть изображена на поверхности тора без точек пересечения, но при этом его проекция на плоскость будет иметь три точки пересечения как проекции пространственных «двойных точек». Физически это означает, что трилистник является элементарной обмоткой поверхности тора — двумерного многообразия, род поверхности которого равен единице. Существуют узлы, которые, аналогично трилистнику, могут быть расположены на других двумерных многообразиях. Так, кольцо — тривиальный узел — располагается в виде обмотки на сфере, а узел «восьмёрка» — на кренделе с двумя дырками. Трилистник может быть представлен в виде двух зеркальных обличий — левого и правого (Рис. 5), топологически не преобразуемых друг в друга.
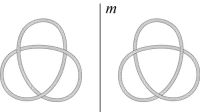 |
Рис. 5. Два зеркальных обличия трилистника
Каждый из них может быть завязан на поверхности тора без контактирующих точек скрещений (Рис. 6(a, b)).
Будучи завязанными вместе на одном и том же торе, они неизбежно будут физически точечно контактировать друг с другом, образуя структуру из двух закрученных в противоположных направлениях замкнутых пространственных спиралей (Рис. 6c).
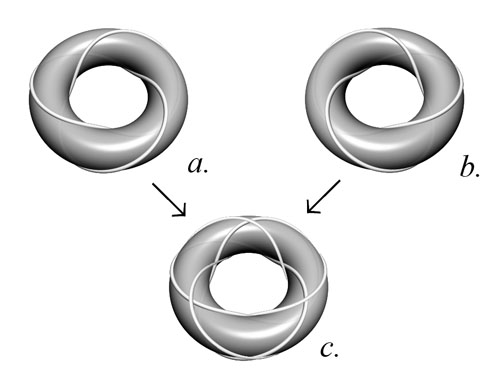 |
Рис. 6(a,b). Правый (a) и левый (b) трилистники по отдельности располагаются на поверхности тора без контактирующих точек
Рис. 6c. Оба трилистника, завязанные на одном и том же торе, имеют между собой точки касания
В результате образуется структура заузленной ткани на поверхности тора. Если оба узла выполнены из упруго-эластичного материала и их скрещения являются реально контактирующими, то вся структура будет представлять собой модель точечной поверхности тора. Здесь важно подчеркнуть, что контактирующие точки определяют модель поверхности, её внешнюю форму, а два зеркальных узла образуют её внутреннюю структуру - структуру-носитель.
Точно таким же образом можно построить модель точечной поверхности произвольного двумерного многообразия, располагая на поверхности тора по меньшей мере два зеркальных крендельных узла соответствующего типа. Это доказывает универсальность данного метода физического моделирования топологических двумерных многообразий в виде точечных поверхностей.
Количество эластичной энергии в заузленном стержне зависит от топологической сложности узла и рассматривается наряду с другими инвариантами узлов [9]. Но в случае применения узлов в качестве структур, задающих точечные модели плоскости, их внутренняя эластичная энергия имеет определяющее значение. Благодаря этой энергии, стремящейся принять наименьшее значение, средняя линия заузленных стержней стремится совпасть с плоскостью, в результате чего все скрещения становятся реально контактирующими, и их множество формирует точечную модель плоскости.
Рассмотренные выше два зеркальных трилистника на поверхности тора, в том случае, если они обладают внутренней энергией упругости, также стремятся сложиться в плоскость, и если бы тор, на который намотаны трилистники, вдруг исчез, то оба узла расположились бы в плоской кольцеобразной области. И наоборот: плоская модель точечной поверхности, заданная циклическим узлом или зацеплением нескольких циклических узлов, в результате приложения к ней внешнего усилия и создания избыточной внутренней энергии упругости, может быть выведена из плоскости, преобразована в пространственное положение и закреплена в нём, чтобы зафиксировать полученную форму.
Главным условием возможности трансформации циклического узла или зацепления из плоскостного положения в пространственное является наличие у него достаточного количества контактирующих скрещений, то есть достаточно детальной аппроксимации плоскости её точечной моделью. Общее число точек скрещений зависит от количества петель циклического узла или зацепления и как следствие — от величины эластичной энергии заузленного упругого стержня. Пропорциональное увеличение числа петель и количества контактирующих скрещений приводит к возникновению у узлов принципиально новых конструктивных свойств. Из простейших узлов наподобие трилистника, они становятся сложными развитыми структурами, которые уже трудно назвать «узлами» в буквальном значении этого слова, то-есть как приспособлениями для завязывания или соединения. На рис. 7(a – f) изображена последовательность циклических узлов, начиная с трилистника, имеющего 3 петли и 3 скрещения. Число петель изменяется согласно натуральному ряду чисел (3, 4, 5, 6, 7, 8, …), при этом соответствующее количество скрещений возрастает согласно арифметической прогрессии второго порядка (3, 8, 15, 24, 35, 48 …). Такие циклические заузленные структуры, созданные специально для моделирования точечных поверхностей, как плоских, так и пространственных, автор предложил называть специальным термином, а именно «NODUS-структуры» (от латинского слова nodus, означающего «узел») [10].
.jpg) |
В процессе трансформации NODUS-структура изменяет площади своих граней, длины рёбер и величины углов между ними, сохраняя лишь инвариант количества точек‑вершин и связность между ними. Благодаря этим особенностям, NODUS-структура способна изменять свою геометрию в целом и образовывать точечные модели поверхностей произвольной гауссовой кривизны: параболической, эллиптической и гиперболической. Эти три типа поверхностей, как известно, полностью исчерпывают все возможные внутренние геометрии двумерных многообразий [11]. Но в противоположность сплошным моделям поверхностей, не способных изменять их гауссову кривизну без разрывов и складок, точечные поверхности NODUS-структур допускают преобразования поверхностей положительной гауссовой кривизны (эллиптические) в поверхности отрицательной гауссовой кривизны (гиперболические) через посредство поверхностей нулевой гауссовой кривизны (параболических). Одна и та же NODUS-структура может принимать формы эллипсоида (Рис. 8a) и однополостного гиперболоида (Рис. 8b). Форма тора (Рис. 8c) образуется как комбинация фрагментов поверхностей положительной и отрицательной гауссовых кривизн с промежуточными областями нулевой кривизны. Возможно также образование точечных моделей и других поверхностей, включая поверхности с самопересечениями и односторонние поверхности.
 |
 |
 | |
a |
b |
c |
Рис. 8(a,b,c). a) NODUS‑структура, моделирующая поверхность эллиптической кривизны; b) Та же структура, но вывернутая наизнанку, моделирует поверхность гиперболической кривизны; c)Модель тора как комбинация фрагментов поверхностей эллиптической и гиперболической кривизны
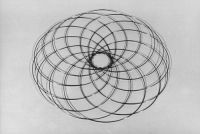
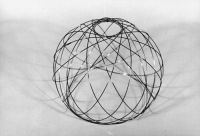
Кроме трансформаций NODUS-структур, изменяющих знак своей кривизны на противоположный, которые могут быть названы «качественной трансформацией», возможен также и другой тип трансформации - «количественный». Этот тип трансформации NODUS-структур осуществляется как постепенное изменение численного значения гауссовой кривизны точечной поверхности от минимального значения до максимального без изменения знака самой кривизны. Минимальное значение гауссовой кривизны может быть равным нулю, и в этом случае точечная поверхность NODUS-структуры аппроксимирует собой фрагмент плоскости. Процесс её трансформации представляет собой непрерывную последовательность изменяющихся форм, например от плоскости к сферическому сегменту, затем к полусфере, а от неё к сфере (Рис. 9(a – e)).
 |
 |
 |
a |
b |
c |
 |
 |
d |
e |
Рис. 9(a-e). Последовательность стадий преобразования NODUS‑структуры из плоскостного положения в сферическое
Такая трансформация является обратимой: сфера может как раскладываться из плоскости, так и вновь складываться в неё без образования разрывов, благодаря уникальным топологическим свойствам моделей точечных поверхностей. Изменяя свою форму, NODUS-структура аккумулирует упругую энергию, напрягается и тем самым увеличивает свою несущую способность (эффект «резильянса»). Любое промежуточное пространственное положение NODUS-структуры может быть зафиксировано посредством ограничения её кинематических свойств тем или иным образом, например посредством дополнительных элементов крепления. В результате трансформируемая NODUS-структура может быть превращена в статичную.
Топологическая сущность NODUS-структур, как конструктивных основ изменяемых точечных поверхностей, позволяет экстраполировать формообразующие возможности их моделей на конструкции больших размеров [12]. Уверенность в возможности такой экстраполяции подтверждается как рядом экспериментов, проведённых автором (Рис. 10(a–c)), так и изучением опыта Р. Б. Фуллера, чьи геометрические структуры одинаково работоспособны, начиная от молекулярного уровня и заканчивая гигантскими куполами‑оболочками пролётом в сотни метров.
 |
 |
 |
a |
b |
c |
Рис. 10(a-c). Экспериментальная модель NODUS‑структуры большого размера в различных стадиях трансформации
Полиморфические кинематические возможности NODUS-структур предоставляют архитектору, инженеру или дизайнеру удобные инструменты не только для поиска требуемых форм в пространстве, но и для органичного «встраивания» их в окружающую среду. Возможно заранее предвидеть сценарий развёртывания плоской точечной модели в поверхность как объект трёхмерного пространства. Такие сценарии могут создаваться посредством различных расположений модульных формообразующих NODUS-структур на плоскости, выбора связей между ними, а также за счёт пространственного расслоения множеств их контактирующих точек.
Являясь в принципе независимым от компьютера, данный метод формообразования и моделирования поверхностей может быть также представлен и в виртуальной форме, для чего потребуется создание специальных компьютерных программ или адаптации уже существующих редакторов трёхмерной графики. Алгоритмический метод анализа упорядоченных точечных множеств, объединённых между собой связующей структурой‑носителем, позволяет ставить вопрос об общем едином способе как виртуального, так и физического моделирования поверхностей в трёхмерном пространстве. При этом физическая природа формообразующих полиморфических NODUS-структур даёт возможность рассматривать их также и в качестве основы реальных кинематических архитектурных конструкций.
Conclusion
Being essentially independent of a computer, the given method of form-finding and modeling of surfaces can be presented also in a virtual aspect by means of creation of special computer programs or adapting already existing 3D editors. The algorithmic method of the analysis of the arranged point sets merged by connected intermediary structure, allows speaking about an uniform method for both virtual and physical modeling of surfaces in three-dimensional space.
The physical nature of form-generating polymorphous NODUS structures allows considering them also as a basis of real-size kinematical architectural structures.
Литература
1. Альберти Л. Б. Десять книг о зодчестве. — М.: Всесоюзная академия архитектуры. Том 1 — 1935. Том 2 — 1937.
2. Лорд И. А., Уилсон С. Б. Введение в дифференциальную геометрию и топологию. Математическое описание вида и формы. — Москва – Ижевск: Институт компьютерных исследований, 2003.
3. Тёрстон У. П., Уикс Дж. Р. Математика трёхмерных многообразий: Пер. с англ. // В мире науки. — 1984. –№ 9. — с. 74 ‑ 88.
4. Чебышев П. Л. О кройке одежды (Sur la Coupe des Vêtements) // Полн. Собр. Соч. П. Л. Чебышева. Том V. — М.‑Л.: АН СССР, 1951. — с. 165 ‑ 170.
5. Otto F. and others. Grid Shells. // Institute for Lightweight Structures (IL-10), University of Stuttgart, Stuttgart 1974
6. Лебедев Ю. С., Рабинович В. И., Положай Е. Д. и др. Архитектурная бионика. — М.: Стройиздат, 1989.
7. Liu L. F., Depew R. E., Wang J. C. Knotted Single-stranded DNA Rings // Journal of Molecular Biology, 1976.-Vol. 106. — p. 439 ‑ 452.
8. Козлов Д.Ю. Регулярные узлы и зацепления – структурный принцип кинематических архитектурных конструкций // «Архитектурная бионика», М., ЦНИИЭПжилища, 1989. — с. 72 ‑ 82.
9. Stewart I. Finding the Energy to Solve a Knotty Problem // New Scientist. March 1993. — p. 18.
10. Kozlov D. Yu. Polymorphous resilient-flexible shaping structures “NODUS” for space and other extreme environments // Final Conference Proceedings Report of The First International Design for Extreme Environments Assembly (IDEEA ONE), University of Houston. Houston, 1991. — p. 259 ‑ 260.
11. Гильберт Д., Кон‑Фоссен С. Наглядная геометрия: Пер. с нем. — М.: Наука, 1981.
12. Kozlov D. Yu. Dome structures for flexible material // Roofs. Part 1. Human settlements and socio-cultural environment. Paris, UNESCO, 1991. — p. 127 ‑ 131.
Issue contents
Содержание журнала















