special EAEA

ARCHITECTURE AND MODERN INFORMATION TECHNOLOGIES

МЕЖДУНАРОДНЫЙ ЭЛЕКТРОННЫЙ НАУЧНО-ОБРАЗОВАТЕЛЬНЫЙ ЖУРНАЛ ПО НАУЧНО-ТЕХНИЧЕСКИМ И УЧЕБНО-МЕТОДИЧЕСКИМ АСПЕКТАМ СОВРЕМЕННОГО АРХИТЕКТУРНОГО ОБРАЗОВАНИЯ И ПРОЕКТИРОВАНИЯ С ИСПОЛЬЗОВАНИЕМ ВИДЕО И КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ

THE COMPUTER METHODS OF CONSTRUCTION SPIRAL STRUCTURES

A.Radzjukewich
NGAHA, Novosibirsk, Russia

Abstract

The object of our research is geometric characteristics of spiral structures which are widely spread in nature (cones, sunflower beds…). It is a well-known fact that there is a proportional intercommunication according to the “golden section”. The correlation of the quantity of “right” and “left” spirals ties to have an irrational coefficient of “golden section” through the correlation numbers of 1,618… from Fibbonacci series ( 5/3, 8/5, 13/8, 21/13, 34/21, 55/34 …). When the proportion of “golden section” was found in the natural objects since the middle of the 19-th century (A.Zeizing), there began to appear a lot of hypotheses about some special aesthetic and technological characteristics of this proportion. The proportion of “golden section” became the most important architectural instrument in the first half of the 20-th century. This instrument made it possible to design beautiful and comfortable buildings (Le Corbusier).

We tried to find a geometric way of building spiral structures which would be similar to natural ones. We solved this problem with the help of the developed algorythm the geometric characteristics of the cells of which spiral structures are built were investigated. It was found out that the cells of “golden” spiral structures don't have any special characteristics if compare with the cells of other spiral structures.

During our work we found some spiral structures which have optimal geometric characteristics. These structures let's call them radial-hexagonal, have maximal area of a cell, though they have minimum perimeter.

We also defined the main difference in the growing strategy of animate and inanimate structures. Inanimate structures grow by means of addition external elements. Animate structures grow by means of constant pushing of new elements which appear in the centre towards periphery. The optimal filling of the plane in the process of such growing is possible only by “golden section” of “right” and “left” spirals.

Keywords: spirals, spiral lattices, a proportion of "gold section”

Spiral structures are studied by lots of sciences, including architectural bionics either [1,2]. Spiral arrangement of seeds, leaves, branches, scales which is called Phyllotaxis is very well known in nature (fig.1).

	Fig. 1. The example of natural Phillotaxis

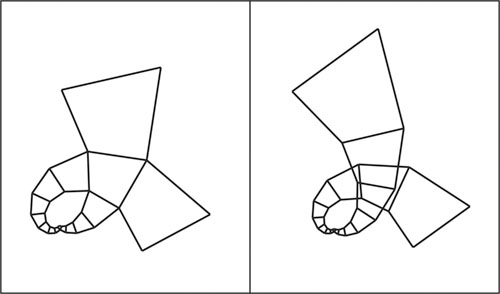
The example of the biological object which can be described as having, spiral structure is sunflower head. The elementary empirical observation gives us an opportunity to suppose that a sunflower head consists of similar quadrangular cells, «growing» from centre to periphery. The question is: is it possible to fill the plane emptylessly with similar geometric figures which are different from each only by scale and angle of turning relative to some central point like it is in a sunflower head? In order to answer this question, we shall try to create some geometric model of building such figures.

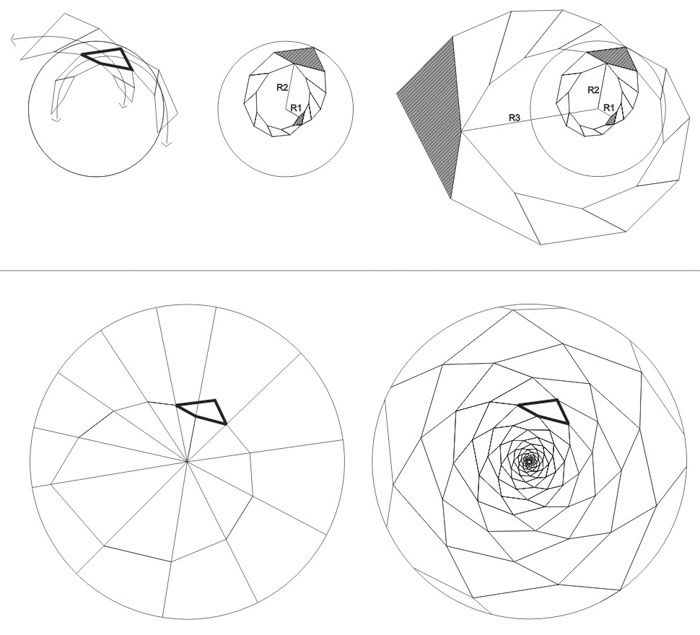
Let`s determine the basic elements of the model by analogy with a sunflower. Let`s suppose that some number of right and left spirals, which are evenly spread by circle line, are built relative to some point calling the pole «O». Let`s believe the spirals to be logarithmic. So we have the plane to be filled with the figures of the same type, which grow from the centre to sides (periphery). Each figure is limited by two neighbouring right and left spirals. These spirals are crossed in four points. If we replace the curvilinear parts of the spirals for the segments which connect the points of crossing of the spirals, we get emptyless filling of the plane with quadrangular «growing» from the centre to periphery (fig. 2).

	Fig. 2. Geometrical modeling of a spiral grid on plane

Let’s see if we can do a mathematical construction of such quadrangular cells of the some type? Let’s have the following parameters:
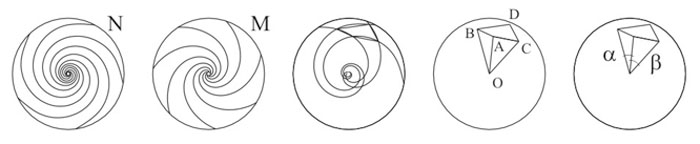
1.Let’s concede that spiral grid is formed on the following base. Let’s call it – «N» of the right logarithmic spirals and «M» - of the left logarithmic spirals (fig. 3);
2.The centre of the spirals or the pole will be named as a letter «O»;
3.The points of the crossing of two pairs of neighbouring right and left spirals will be named as letters A, B, C, D;
4.Let’s name angle , angle , having and

	Fig. 3. Geometric modeling of a spiral grid’s cell

Let’s watch the conditions when the quadrangular A B C D can be a figure which allows to fill the plane emptylessly like seeds fill a sunflower head. Our investigation showed that we must have four of these conditions:
1.The triangle O A B must be equal to the triangle O C D;
2.The triangle O A C must be equal to the triangle O D B;
3. ;
4.

Only following these conditions, multiple scale copying of the quadrangular A B C D which moves clockwise and anticlockwise will allow to fill the plane emptylessly (fig. 4).

	Fig.4. Geometric building of spiral grid, filling the plane

We should say that copying of the given (original) quadrangular for «N» times clockwise and «M» times anticlockwise will have the spirals closed. If we go on copying, we shall get a new circuit with new closing of the spirals. The distance from the quadrangular to the spirals pole «O» will be changed constantly:

Let’s call this magnitude as a coefficient of growing of the spiral grid. If we do not observe the given condition we shall not get the «closing» of the spirals (fig. 5).

	Fig. 5 The example of geometric filling of plane with a spiral grid witр any parameters

The number of quadrangular cells which follow the given conditions is unlimited. We can form a cell which will fill the plane emptylessly when being copied. And it doesn’t matter what meanings «M» and «N» will have and what meaning the coefficient will have. It should be said that the cells in the spiral grids may be of three types: protuberant quadrangular, concave quadrangular and in the case of placing the segments AB and AC along the straight line – triangular (fig. 6).

	Fig. 6. The examples of spiral grids having different forms of cells

Let’s have some limited conditions in order to form spiral grids. We shall form a pattern where the points of the crossing of the spirals tops of cells will be the centers of circles. Let’s call them balls with their centers in one plane (platitude). In this case we also can build unlimited number of spiral grids when observing some certain conditions. We made an algorythm of calculation which is based on solution of rather complete system of trigonometric equations in order to calculate the geometric parameters of such grids. The automatic calculation was made with the help of the software (computer program) MatCAD (the author of this algorythm is Scherbatykh S. V.) The results which we received became the base for drawing the grids. The problem of labour – intensiveness of geometric formations was solved with the help of automatization of this process using the software AutoLIPS of the program AutoCAD (the author of the algorythm is Moroz S.A.)

When N, M meanings are fixed, the value of the coefficient of spirals growing may be changed but only within definite limits. The limits appear when there is a contact of the balls placed in the opposite tops of the cell. In this case pole – tetragonal structure turns into pole – hexagonal one and we get only two variants of apportionment of balls. In the first case there is a contact between the nearest and the farthest balls, relative to the centre of the spirals. In the second case we have the contact between the side ones.

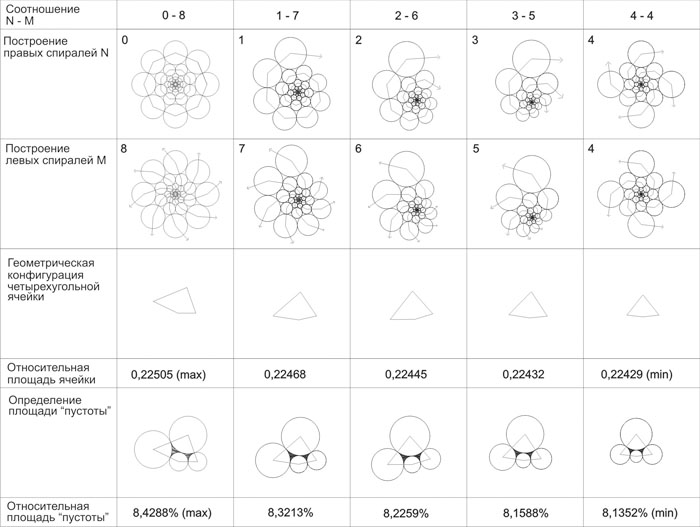
Let’s see what the peculiarities and characteristics of the pole – hexagonal spiral grids are. Suppose that the sum of right and left spirals is a constant value and is equal to eight. In this case we have nine variants of construction of spiral grids:

1) 8M(4) – 0N(4);
2) 7M(4) – 1N(4);
3) 6M(4) – 2N(4);
4) 5M(4) – 3N(4);
5) 4M(4) – 4N(4);
6) 3M(4) – 5N(4);
7) 2M(4) – 6N(4);
8) 1M(4) – 7N(4);
9) 0M(4) – 8N(4).

If we remove symmetrical variants we shall have only five ones:

1) 8M(4) – 0N(4);
2) 7M(4) – 1N(4);
3) 6M(4) – 2N(4);
4) 5M(4) – 3N(4);
5) 4M(4) – 4N(4).

The first case we can hardly name as a spiral grid, because there almost is not a spiral in one direction and it turns into a circle. Anyway, we shall examine this case to have the whole picture of all typological cases because this structure is a radial one. This is interesting from the point of view of an examiner because a lot of historical cities have the same town – planning structure.

We tried to determine how some geometric characteristics of different spiral grids relate to each other. In particular we examined how perimeters of the cells relate to their squares (fig. 7). The perimeter was divided by square root of cell squares in order to measure these magnitudes, longitude and square. The results revealed that the cell of the spiral grid which has different number of right and left spirals (N=0, M=8) has relative maximum square. It is obvious that increasing of M-meaning will lead to increasing of a relative cell square as it will tend to a form of right hexagonal being within a limit.
Also, we examined how the square of the «emptyness» which is formed between the cell circles relates to the square of the cell itself. We found out that the relative square of the emptiness was minimal inside the spiral grid where N=M (let's call it symmetrical spiral grid).
Therefore these very symmetrical spiral grids have the highest density of balls arrangement (fig. 7).

	Fig. 7. Comparing of geometrical parameters of spiral grids

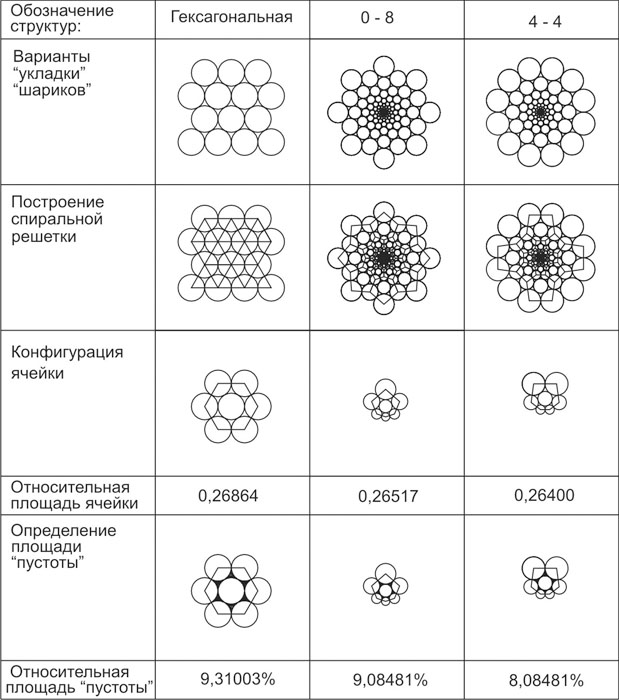
It should be mentioned that, the cells inside the natural objects may have a hexagonal form as daisy head has and not a quadrangular. Here we have pole-cell structure of elements arrangement. The calculation algorythm of building spiral pole-hexagonal structures, which we got, gives us an opportunity to build spiral structures made of hexagonal. On the analogy of building different spiral grids based on quadrangular cells we shall build spiral grids based on hexagonal cells (fig. 7).

The check of geometric characteristics of hexagonal cells revealed that they are identical to the parameters of the cells built on the base of quadrangular cells. The minimal square of emptinesses relative to the hexagonal cell was the same, as it had been earlier, when the number of right and left spirals was equal. Maximal square of hexagonal cell relative to the perimeter was the same when the correlation of opposite spirals is absolutely different (N=0, M=8).
It should be mentioned, that depending on certain given conditions, hexagonal cells like quadrangular cells may have both protuberant and concave forms and moreover if two sides of the hexagonal are on the same straight line, this hexagonal may turn into pentagon.

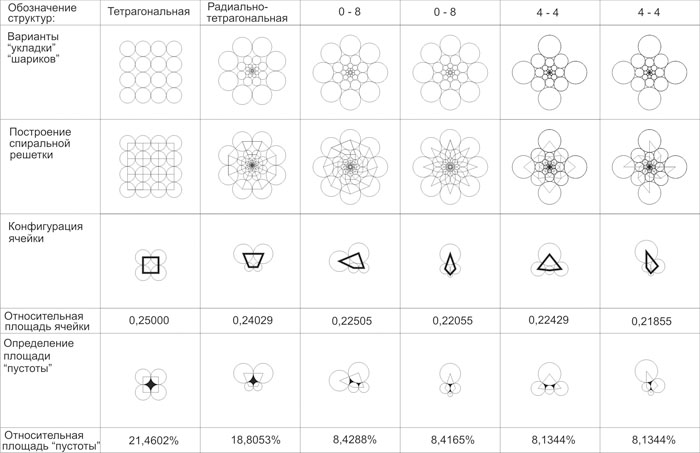
Now, we have one more question to answer: is it possible to solve a problem of finding an ideal town – planning structure, where the length of roads will be minimal relative to squares of the sites, enclosed by these roads. It is obvious, that according to Deсart coordinate system two structures – tetragonal and hexagonal which are based on a square and a right hexagonal, will be ideal. In the first case the relative square of the site will be 0,25 of unit, and in the second one 0,26864 of unit.If we examine all the pole-tetragonal (fig.8) and pole-hexagonal (fig. 9) spiral structures, which have extreme parameters, we shall get the spiral structure with the number of spirals N=0 and M=8 as the optimal one. Let's call it radial-hexagonal. In this case, the relative square of the cell will be maximal in comparison with all other variants - 0,26517.

	Fig. 8. Comparing of the geometrical parameters of radial-tetragonal spiral grids
	Fig. 9. Comparing of the geometrical parameters of radial-hexagonal spiral grids

It is inferior to hexagonal structure only 1,3% and excels tetragonal structure 5,7%. Such exceeding must be considered rather significant if we want to solve town-planning problems. There must be a definite economic sense in such a theoretical approach. More over, we can find a similar solution which was offered by Italian architect Antonio Filarete in 15th century, in the ideal city Sforcindy [3] (fig. 10).

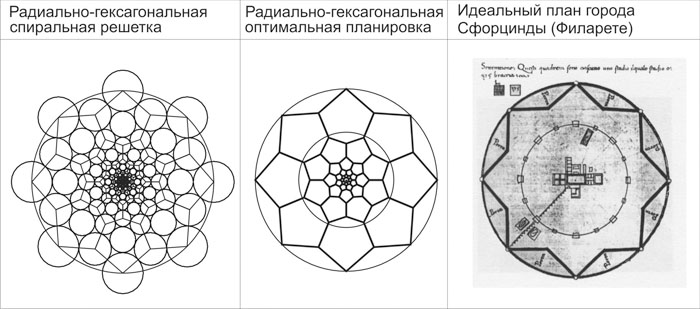	Fig. 10. Comparing of the optimal radial-hexagonal spiral structure with the plan of the ideal town Sforcindy (A.Filarete)

We also compared geometric parameters of different spiral grids in order to reveal some extreme (maximal or minimal) meanings. Spiral grids with correlation of the number of opposite spirals which (correlation) was similar to «golden section» were especially interesting. But after examining all the variants, the one which was nearest to «golden section» (N=3, M=5) was not extreme one by the definite parameters. So, the arrangement of seeds in natural conditions (nature) can't be considered as absolutely dense. We can't also affirm that the square of the cell (quadrangular or hexagonal) is absolutely maximal relative to the size of the perimeter of the cell.

In conclusion we can say that this very work makes it possible to solve a lot of different architectural and design problems. For example, the method which was developed to calculate forms of the cells will allow sorting out the process of geometric structure and forming in different fields of design (ornament, decoration, etc.). Also, this method can be used in town planning. After examining different geometric structures we can affirm that radial-hexagonal structures are the most optimal, if consider the minimal length of perimeters (roads, ways, utility lines). By the way here we get maximal relative square of cells (blocks and districts).

There appears one more question: why hasn't nature chosen a radial-hexagonal structure to form alive objects? It is probably because here we meet different strategies of structures growth. If we consider the process of city growth we can affirm that they are based on simultaneous growth in different directions from the centre to periphery. And in this case we have an annexation of new territory. Crystals probably grow the same way. But the growing process in heads of sunflowers goes different way. There is growing of new seeds in the centre of a sunflower head, this growing passes through equal periods of time, and these seeds are pushed by new- born seeds into the sector of the head, which is freer from other seedy. This process can be seen at the website [4] where there is a film made with the help of program (FBN1NB). Mathematical modeling of this process [5] showed that the optimal filling of sunflower head happens when spiral grids with the correlation of the number of right and left spirals is like the proportion of «golden section» are formed. The main difference between the processes of growing crystals and the same of biological structures is that in the first case it happens an «annexation» (addition) of new elements from the outside, and in the second case there is pushing of a new element from the centre to periphery.

References

1. Шубников А.В., Копцик В.А. Симметрия в науке и искусстве. Издание третье, дополненное. М.2004.

2. Архитектурная бионика. Под ред. Лебедева Ю.С. М. Стройиздат.1990.

3. Филарете (Антонио Аверлино). Трактат об архитектуре. Пер/прим. В.Л.Глазычев. Изд.”Русский университет”. М. 1999.

4. http://www.brantacan.org.uk/programs.htm

5. Щетников А.И. Проблемы филлотаксиса. http://www.nsu.ru/classics/pythagoras/Phyllotaxis.pdf

Download at PDF

Issue contents